Comme quelque chose de barbant, qui peut devenir amusant ! Comme quelque chose de barbant, qui peut devenir amusant !
Réduction d’expressions comprenant des puissances
Réduction d’une puissance d’un produit
Soit le produit des nombres x et y, élevé à la troisième puissance.
En L.M. :
| (x . y)3 | |
| La définition de la puissance nous permet d’écrire : | = (x . y) . (x . y) . (x . y) |
| Vu l’associativité de la multiplication, on a : | = x . y . x . y . x . y |
| Vu la commutativité de la multiplication, on a : | = x . x . x . y . y . y |
| Vu l’associativité de la multiplication, on a : | = (x . x . x) . (y . y . y) |
| La définition de la puissance nous permet d’écrire : | = x3 . y3 |
| D’où : (x . y)3 = x3 . y3 | |
Nous retiendrons la formule :
| ∀ x, y ∈ Q ; ∀ n ∈ N : (x . y)n = xn . yn |
Réduction d’une puissance de puissance
Soit la 2e puissance de x élevée à la 3e puissance.
En L.M. : (x2)3
| La définition de la puissance nous permet d’écrire : | = (x2) . (x2) . (x2) |
| La définition de la puissance nous permet d’écrire : | = (x . x) . (x . x) . (x . x) |
| Vu l’associativité de la multiplication, on a : | = x . x . x . x . x . x |
| La définition de la puissance nous permet d’écrire : | = x6 |
D’où : (x2)3 = x6
Nous retiendrons la formule :
| ∀ x ∈ Q ; ∀ m, n ∈ N : (xm)n = xm . n |
Réduction d’un produit de puissances de même base
Soit le produit de la 2e puissance de x, par la 3e puissance de x
En L.M. : x2 . x3
| La définition de la puissance nous permet d’écrire : | = (x . x) . (x . x . x) |
| Vu l’associativité de la multiplication, on a : | = x . x . x . x . x |
| La définition de la puissance nous permet d’écrire : | = x5 |
D’où : x2 . x3 = x5
Nous retiendrons la formule :
| ∀ x ∈ Q ; ∀ m, n ∈ N : xm . xn = xm+n |
Réduction d’une puissance d’un quotient
Soit le quotient de x par y noté (x/y) élevée à la 3e puissance.
En L.M. : (x/y)3
| La définition de la puissance nous permet d’écrire : | = (x/y).(x/y).(x/y) |
| La règle du produit de fractions nous permet d’écrire : | = (x.x.x)/(y.y.y) |
| La définition de la puissance nous permet d’écrire : | = x3/y3 |
D’où : (x/y)3 = x3/y3
Nous retiendrons la formule :
| ∀ x ∈ Z ; ∀ y ∈ Z0 et ∀ n ∈ N : (x/y)n = xn/yn |
Réduction d’un quotient de puissances de même base
1er cas :
Soit le quotient de la 5e puissance de x, par la 3e puissance de x
En L.M. : x5/x3
| La définition de la puissance nous permet d’écrire : | = (x.x.x.x.x)/(x.x.x) |
| En appliquant la simplification de fractions, on a : | = (x.x)/1 |
| La définition de la puissance nous permet d’écrire : | = x2 |
D’où : x5/x3 = x2
2ème cas :
Soit le quotient de la 3e puissance de x, par la 5e puissance de x
En L.M. : x3/x5
| La définition de la puissance nous permet d’écrire : | = (x.x.x)/(x.x.x.x.x) |
| En appliquant la simplification de fractions, on a : | = 1/(x.x) |
| La définition de la puissance nous permet d’écrire : | = 1/x2 |
D’où : x3/x5 = 1/x2
Nous retiendrons la formule :
∀ x ∈ Z0 ; ∀ m, n ∈ N :
|
Remarque :
| x0 = 1 sauf si x = o (expression indéterminée) |
Divisions de fractions rationnelles
Exemple de division de fractions rationnelles(les conditions d’existence sont supposées vraies):
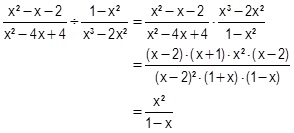
Vidéo présentant quelques exemples (attention, les méthodes de factorisation évoquées sont différentes de celles vues en classe)
Repérage dans un plan
Repère cartésien : description
Pour repérer un point dans un plan et par la suite (les fonctions) représenter une relation entre deux variables, le système le plus souvent utilisé est le repère cartésien. Il en existe d'autres qui ne seront pas développés ici : coordonnées polaires,...
Un repère cartésien est défini par :
- deux droites graduées, perpendiculaires;
- leur intersection appelée origine du repère;
- quatre quadrants, les quatre régions du plan que ces droites délimitent.
Axe horizontal
L'axe horizontal d'un plan cartésien se nomme l'axe des abscisses , ou l'axe des x. Cet axe gradué est orienté de la gauche vers la droite dans le plan cartésien (on y indique la valeur de la variable indépendante dans une relation entre deux variables).
Axe vertical
L'axe vertical d'un plan cartésien se nomme l'axe des ordonnées , ou l'axe des y. Cet axe gradué est orienté du bas vers le haut du plan cartésien (on y indique la valeur de la variable dépendante dans une relation entre deux variables).
L'origine du repère
L'intersection des deux droites graduées est appelée origine du repère. Elle est notée O et ses coordonnées sont (0 ; 0).
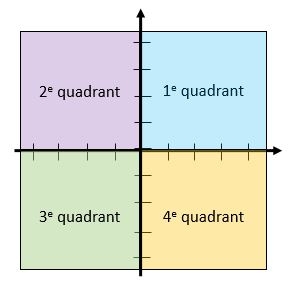
Les quatre quadrants
Les quatre régions du plan délimitées par ces deux axes sont appelées quadrants.
Ils sont numérotés dans le sens anti-horloger.
Coordonnées d'un point
La graduation des axes du plan cartésien permet de situer des points dans un plan. La position d'un point est donnée par un couple de nombres :
- le premier nombre s'appelle l'abscisse du point;
- le second nombre est appelé ordonnée du point.
Ensemble, ils forment un couple de nombres appelé les coordonnées du point et noté (x ; y).
Le premier nombre du couple correspond à la position horizontale du point (sa valeur sur l'axe des x ) alors que le deuxième nombre correspond à sa position verticale (sa valeur sur l'axe des y ).
Exemple : quelles sont les coordonnées du point A dessiné ci-dessous ?
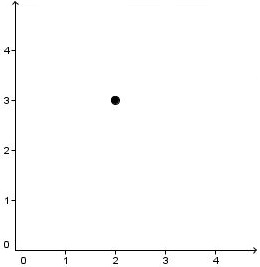
En partant de l'origine du repère, sur l'axe des x, il faut se déplacer de 2 unités vers la droite : l'abscisse du point A vaut "2".
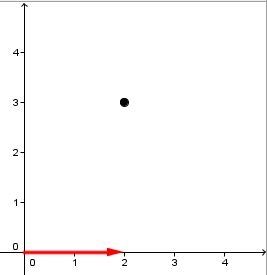
De là, il faut monter de 3 unités vers le haut, parallèlement à l'axe des y, pour atteindre le point A : l'ordonnée du point A vaut "3".
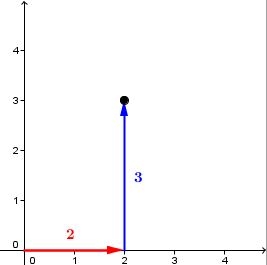
Conclusion : les coordonnées du point A sont (2 ; 3).
Notion de fonction
Additions et soustractions de fractions rationnelles
Exemple d'addition-soustraction de fractions numériques (rappel)
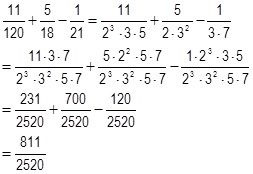
Exemple d'addition-soustraction de fractions rationnelles (les conditions d'existence sont supposées vraies)
Exemple 1 :
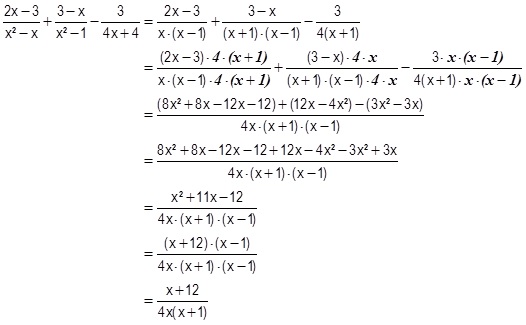
Exemple 2
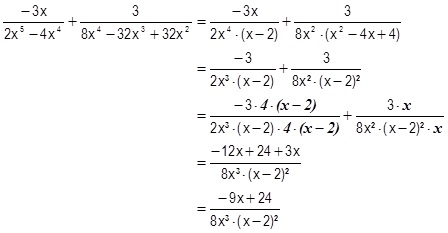
Vidéo présentant quelques exemples (attention, les méthodes de factorisation évoquées sont différentes de celles vues en classe)