Vocabulaire et notations
- Une inéquation est une inégalité (> ; < ; ≤ ; ≥) qui renferme au moins une inconnue.
- Résoudre une inéquation c’est trouver toutes les valeurs de l’inconnue qui vérifient l’inégalité. Ces valeurs sont appelées solutions de l’inéquation.
- Convention d’écriture (a et b sont des réels):
| L'écriture | signifie que |
|
a < b |
a est strictement plus petit que b |
|
a > b |
a est strictement plus grand que b |
|
a ≤ b |
a est soit plus petit , soit égal à b |
|
a ≥ b |
a est soit plus grand , soit égal à b |
 Résolution d'inéquations
Résolution d'inéquations
|
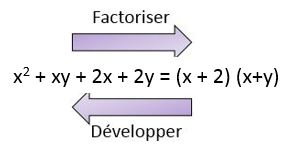
La factorisation est la transformation d'une expression algébrique (somme ou différence) en un produit de facteurs. |
Généralement, la factorisation permet de transformer une expression algébrique afin de résoudre un problème plus facilement. Les facteurs obtenus après la factorisation sont des polynômes de degré inférieur (ou égal) au polynôme de départ.
La factorisation de polynômes permet entre autres de :
- résoudre des équations d’un degré supérieur à 1 ;
- se donner des outils pour le calcul des fractions algébriques ;
- préparer la détermination de zéros et l’étude du signe de fonctions polynomiales (principalement en 4ème année).
L'opération inverse à la factorisation se nomme le développement d'une expression algébrique.
 Mise en évidence
Mise en évidence
 Différence de deux carrés
Différence de deux carrés
 Trinôme Carré Parfait
Trinôme Carré Parfait
 Trinômes "non carrés parfaits" - "Méthode des rectangles"
Trinômes "non carrés parfaits" - "Méthode des rectangles"
 Groupement "deux-deux"
Groupement "deux-deux"
 Tableau synthèse des méthodes de factorisations
Tableau synthèse des méthodes de factorisations
Tu as souvent rencontré des expressions telles que celles écrites ci-dessous :
3x – 2 ; 9 – t² ; 4x² - 5x + 2 ; ; 4a²b³ ; 5x ; -6 ; …
Ces expressions sont toutes des polynômes.
Chacun des termes d’un polynôme s’appelle un monôme[1].
Prenons un polynôme :
P1(x) = 4x² - 5x + 4
- Il est du deuxième degré en « x » car le plus grand exposant de « x » est 2.
- Il est ordonné et complet.
- « 4 » est son terme indépendant.
Remarque : -6 est un monôme de degré 0.
Prenons un deuxième polynôme :
P2(t) = 4t² - 5,3t³ + 4
- Il est du troisième degré en « t » ;
- il n’est pas ordonné;
- il est incomplet parce qu’il n’a pas de terme du premier degré.
Ordonnons-le :
- par rapport aux puissances décroissantes de t :
P2(t) = -5,3t³ + 4t² + 4
- par rapport aux puissances croissantes de t :
P2(t) = 4 + 4t² - 5,3t³
 Polynômes : vocabulaire
Polynômes : vocabulaire
 Division Euclidienne de polynomes
Division Euclidienne de polynomes
Des mathématiciens allemands et italiens ont imaginé, au début du XXè siècle, le regroupement de différents nombres ayant les mêmes caractéristiques en ensembles ou familles de nombres.
Les ensembles de nombres sont les suivants :
Les entiers naturels :
N = {0 ; 1 ; 2 ; 3 ; …}
C'est l'ensemble des nombres qui servent à compter, à dénombrer. L'ensemble N fut crée par Peano (1858-1932), et c'est de « naturale » en italien que provient la lettre N.
Les entiers relatifs
Z = {… ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; …}
C'est l'ensemble des entiers positifs ou négatifs, ceux qui n’ont pas de partie décimale. Le Z, vient de zahl (nombre) et zalhen (compter) en allemand, langue de son « inventeur » : Dedekind(1831-1916).
Les nombres rationnels
Q = {… ; ½ ; -3/5 ; -4 ; … ; 0 ; 1,77…7… ; -12,45858…58… ; -2 ; …}
C’est l’ensemble des nombres qui peuvent s'écrire sous la forme d'une fraction à termes entiers. C'est encore Peano qui inventa cet ensemble, Q venant de « quotiente » en italien.
Cet ensemble regroupe :
- Les nombres entiers, en effet, tout nombre entier peut s’écrire comme une fraction dont le numérateur est cet entier et le dénominateur 1 (ex. : -7 = -7/1)
- Les nombres décimaux limités qui peuvent être représentés par une fraction dont le numérateur est ce nombre auquel on a ôté la virgule et le dénominateur la puissance de 10 correspondant au nombre de décimales (ex. : 12,237 = 12237/1000)
- Les nombres décimaux illimités périodiques qui, par un petit raisonnement, peuvent être transformés en une fraction à termes entiers :
Ex. : Transformer le nombre périodique n = 2,142727…27…en fraction.
On multiplie « n » par une puissance de 10 (10, 100, 1000, etc.) de façon à déplacer la virgule à droite de la première période :
On multiplie ensuite « n » par une puissance de 10 de façon à déplacer la virgule à gauche de la première période (si il n’y a pas d’antipériode - ici 14-, on multiplie n par 1):
On soustrait membre à membre les deux équations des étapes 1 et 2 : les membres de gauche de l'égalité sont soustraits entre eux, les membres de droite entre eux aussi. Ainsi, les parties décimales illimitées sont identiques et la différence de droite est un nombre entier :
10000n - 100n = 21427,2727…27… - 214,2727…27…
Soit 9900n = 21213
Pour trouver la valeur de « n » sous forme fractionnaire, on divise le nombre entier obtenu à droite de l’égalité par le coefficient de « n » (on isole n) :
n = 21213/9900
Nous avons ainsi la valeur de n, mais en notation fractionnaire, où le numérateur est 21213 et le dénominateur est 9900. Si on effectue la division de 21213 par 9900, on retrouvera notre nombre décimal périodique de départ.
La fraction recherchée est donc :
21213/9900
On peut éventuellement simplifier cette fraction:
2357/1100
 Vidéo de Khan Academy sur le sujet
Vidéo de Khan Academy sur le sujet
Les nombres irrationnels
Par opposition aux nombres rationnels, il s’agit de l’ensemble des nombres décimaux qui ne peuvent être transformés en une fraction à termes entiers. Les deux plus connus sont : « ∏ » et « e »
- Les premières décimales de π sont :
3,14159265358979323846264338327950288419716939937510582…
Mais dans la pratique, on utilise le plus souvent 3,14. Les décimales de « ∏ » ont été la proie des savants depuis près de 4000 ans.
- Le nombre « e » ne fait son apparition qu’au XVIIe siècle avec le développement des logarithmes. Ses premières décimales sont :
2,71828182845904523536028747135266249775724709369995957…
- Un autre nombre irrationnel connu est le nombre d’or : Φ = (1 + V5)/2 soit approximativement 1,6180339887
C’est dans cet ensemble qu’on retrouvera la plupart des radicaux envisagés dans ce chapitre.
 Accès au note du cours
Accès au note du cours
I = {… ; - ; π ; ; …}
Les nombres réels
R = Q ∪ I
C'est l'union des ensembles Q et I, soit tous les nombres "réels". R pour « real », cet ensemble a aussi été crée par Dedekind.
Les nombres complexes
Ensemble des nombres de la forme "a + ib" (avec i² = -1). L'emploi de la lettre C provient sans doute d'une convention logique dans la lignée des autres.
 Notion de base
Notion de base
 Valeur approchée
Valeur approchée
 Simplifier des radicaux numériques
Simplifier des radicaux numériques
 Additionner et soustraire des radicaux
Additionner et soustraire des radicaux
 Développer une expression
Développer une expression
 Rendre un dénominateur rationnel
Rendre un dénominateur rationnel