Les projections parallèles
Les ombres
Comme les rayons du soleil viennent d’un astre très éloigné, on peut les considérer comme parallèles. C’est pourquoi, quand un objet est exposé au soleil, tous les segments joignant chacun des points de l’objet au point de son ombre sont parallèles.
Propriétés des ombres au soleil
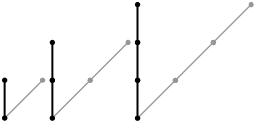
- Si un bâton est placé dans la direction des rayons du soleil, son ombre est réduite à sa base.
- Les ombres de deux bâtons parallèles entre-eux sont parallèles entre-elles. En plus :
- Si les bâtons ont même longueur, leurs ombres ont la même longueur ;
- Si un bâton a une longueur double de l’autre, l’ombre du 1er à une longueur double de celle du 2ème.
Règle graduée et projection parallèle
Les propriétés des projections parallèles (des ombres) expliquées ci-dessus peuvent s’appliquer à la droite graduée.
| Les projections parallèles conservent les abscisses |
- Remarque importante : si les abscisses sont conservées, les longueurs des segments ont été multipliées par un même nombre qui est le rapport entre la longueur d’un segment-image et la longueur de son correspondant.
Division d’un segment en parties égales
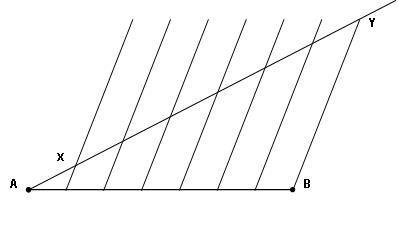
On peut utiliser la propriété précédente pour diviser un segment en parties égales. Divise, par exemple, le segment [AB] en 7 parties égales :
- Trace une demi-droite d’origine A.
- Place sur cette demi-droite un point X.
- Reporte ce segment [AX] six fois au-delà de B.
- Appelle Y ce dernier point. Tu obtiens ainsi une graduation de [AY].
- Projette cette graduation sur [AB] parallèlement à la droite YB.
Compte tenu de la propriété énoncée ci-dessus, cette nouvelle graduation divise le segment [AB] en 7 parties égales.
Conservation du milieu
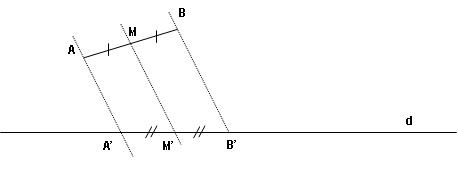
Considérons le segment [AB] et le point M, milieu de ce segment. Si on projette ce segment sur une droite d dans une direction quelconque, on obtient le segment [A’B’] où M’ (image de M) est aussi le milieu de [A’B’] :
| Toute projection parallèle conserve le milieu |
Cette propriété appliquée au cas particulier des triangles porte le nom de théorème du milieu :
| Dans un triangle, la droite passant par le milieu d’un côté et parallèle à un autre côté passe par le milieu du troisième côté |