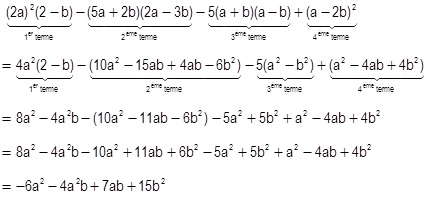Notion

Développer une expression algébrique, c'est la transformer en une somme d'un nombre minimum de termes.

Marche à suivre

Pour ce faire (à ce stade de la matière), comme dans le calcul numérique, tu dois respecter les priorités opératoires :

1. Les parenthèses

Ces parenthèses indiquent ce qu’il faut d’abord calculer. A l’intérieur de celles-ci, on respectera l’ordre de priorité décrit dans cette synthèse.

2. Les puissances

• (x + y)² = x² + 2.x.y + y² ou (x - y)² = x² - 2.x.y + y²
• (x/y)ⁿ = xⁿ/yⁿ
• (x.y)ⁿ = xⁿ.yⁿ
• (x^m)ⁿ = x^m.n
• xⁿ = x.x.....x

3. Les produits

• (x + y).(x - y) = x² - y²
• x.(y ± z) = x.y ± x.z ou (x + y).(a + b) = ax + bx + ay + by
• x^m.xⁿ = x^m+n

• Recopier les facteurs littéraux de chaque terme dans l’ordre alphabétique.

• Calculer les produits de facteurs numériques et les placer en tête des monômes.

4. S’il reste des parenthèses, appliquer une des quatre formules suivantes :

• x + (y + z) = x + y + z
• x + (y - z) = x + y - z
• x - (y + z) = x - y - z
• x - (y - z) = x - y + z

5. Les sommes algébriques de termes semblables (et uniquement s’ils sont semblables).

En pratique...

Soit à déveloper puis réduire l'expression suivante :

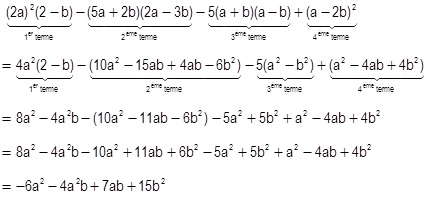
En pratique... :

1. « Découper » l'expression algébrique en termes.
2. Dans chaque terme, respecter les priorités opératoires comme décrites dans la théorie ci-dessus. Dans l'exemple :

• 1er terme : puissance puis simple distributivité
• 2ème terme : double distributivité
• 3ème terme : produit de deux binômes conjugués puis simple distributivité
• 4ème terme : carré d'un binôme.

3. Appliquer les règles des parenthèses s'il en reste (4).
4. Additionner les termes semblables et uniquement les termes semblables (5).

Rappel : applications des produits remarquables

Explications simples à partir d'exemples

Exercices

Exercices de rapidité : produits remarquables  

Exercices de développement d'expressions algébriques