Comme quelque chose de barbant, qui peut devenir amusant ! Comme quelque chose de barbant, qui peut devenir amusant !
Croissance et décroissance
Exercices sur le site de Khan Academy
Quand tu parcours le « tracé » d’une fonction de gauche à droite (pour des valeurs de « x » croissantes), la courbe « monte » ou « descend ». On dit que la fonction est croissante ou décroissante.
En cinquième année, tu apprendras à déterminer par calcul sur quels intervalles une fonction est croissante, décroissante ou constante. Ici, nous allons nous contenter de dresser un tableau de variation de fonction à partir de son graphique.
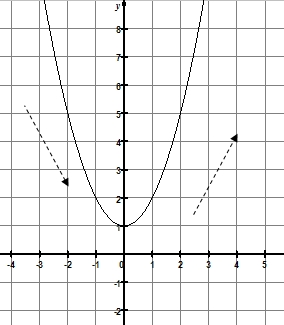
| Une fonction est croissante sur un intervalle si lorsque les valeurs de « x » croissent, les valeurs de f(x) ou y croissent aussi (« quand on se déplace vers la gauche, la fonction monte ») |
Dans l’intervalle ]0 ; +∞[, quand les « x » augmentent, les « y » augmentent aussi
| Une fonction est décroissante sur un intervalle si lorsque les valeurs de « x » croissent, les valeurs de f(x) ou y décroissent (« quand on se déplace vers la gauche, la fonction descend ») |
Dans l’intervalle ]-∞ ; 0[, quand les « x » augmentent, les « y » diminuent
Tableau de variation de la fonction ci-dessus :
| x | -∞ | 0 | +∞ | ¬ Maximum et minimum locaux |
| y | æ |
1 minimum en (0 ; 1) |
ä | |
Maximum ou minimum local
Remarque :
Quand l’ordonnée d’un point est supérieure à celles des points du graphique d’une fonction, situés dans son voisinage, on dit que ce point est un maximum local (ce n’est pas nécessairement le point le plus « haut » du graphique de la fonction). Le point « le plus haut » du graphique est appelé maximum absolu.
Quand l’ordonnée d’un point est inférieure à celles des points du graphique d’une fonction, situés dans son voisinage, on dit que ce point est un un minimum local (ce n’est pas nécessairement le point le plus « bas » du graphique de la fonction). Le point « le plus bas » du graphique est appelé minimum absolu .
Exercices sur le site de Khan Academy
Tableau de variation d'une fonction
Exemple :
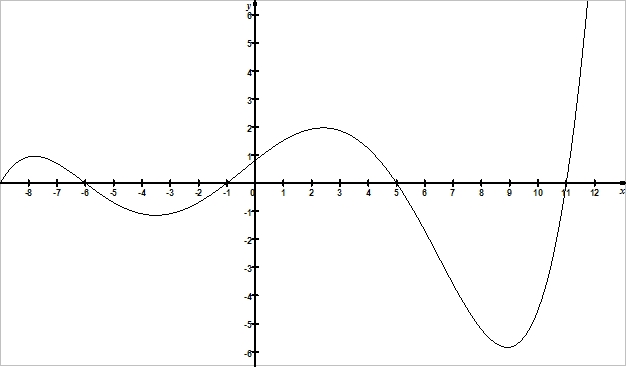
La fonction est strictement croissante pour :
x Î ]-9 ; -7,8[ U ]-3,5 ; 2,5[ U ]9 ; +¥[
La fonction est strictement décroissante pour :
x Î ]-7,8 ; -3,5[ U ]2,5 ; 9[
Tableau de variations de la fonction représentée ci-dessus :
| x | -7,8 | -3,5 | 2,5 | 9 | ¬ Extrémum | |||||
| y | ä |
1 Maximum en (-7,8 ; 1) |
æ | -1 minimum en (-3,5 ; -1) | ä |
2 Maximum en (2,5 ; 2) |
æ | -6 minimum en (9 ; -6) | ä |
Exercices sur le site de Mathématiques.org