Comme quelque chose de barbant, qui peut devenir amusant ! Comme quelque chose de barbant, qui peut devenir amusant !
Pente d'une droite à partir d'un graphique
Calcul de la pente d'une droite passant par deux points
Exercices sur le site de Khan Academy
Droites paralleles
- Deux droites verticales sont parallèles entre-elles et ont des équations du type : x = p et x = q.
- Deux droites horizontales sont parallèles entre-elles (leur pente = 0) et ont des équations du type : y = p et y = q.
- Deux droites obliques parallèles ont la même pente et ont des équations qui ne différent que par leur terme indépendant :
| d1 // d2 <=> pente de d1 = pente de d2 |
|
d1 ≡ y = m.x + p et d2 ≡ y = m.x + q |
Droites perpendiculaires
Si une droite est verticale et l’autre horizontale, elles sont perpendiculaires entre-elles. Leurs équations respectives sont du type : y = p et x = q.
Pour déterminer le lien entre les pentes de deux droites perpendiculaires non parallèles aux axes, il faut observer la situation ci-dessous :
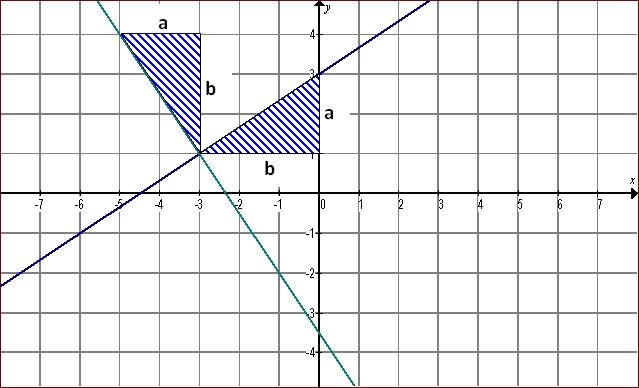
- Une des droites « monte » (d1 en bleu) et l’autre « descend » (d2 en vert), leur pente sont donc de signes contraires.
- Les deux triangles construis pour déterminer leur pente respective sont isométriques (rotation de 90°).
md1 = a/b et md2 = -b/a (aveca et b deux nombres positifs non nuls)
Dans un repère orthonormé, si deux droites obliques sont perpendiculaires, la pente de l’une est l’opposé de l’inverse de la pente de l’autre :
| d1 ⊥ d2 <=> pente de d1 = -1/pente de d2 |
|
d1 ≡ y = m.x + p et d2 ≡ y = (-1/m).x + q |
