Comme quelque chose de barbant, qui peut devenir amusant ! Comme quelque chose de barbant, qui peut devenir amusant !
Repérage dans un plan : rappel des notions de première année
Repère cartésien : description
Pour repérer un point dans un plan et par la suite (les fonctions) représenter une relation entre deux variables, le système le plus souvent utilisé est le repère cartésien. Il en existe d'autres qui ne seront pas développés ici : coordonnées polaires,...
Un repère cartésien est défini par :
- deux droites graduées, perpendiculaires;
- leur intersection appelée origine du repère;
- quatre quadrants, les quatre régions du plan que ces droites délimitent.
Axe horizontal
L'axe horizontal d'un plan cartésien se nomme l'axe des abscisses , ou l'axe des x. Cet axe gradué est orienté de la gauche vers la droite dans le plan cartésien (on y indique la valeur de la variable indépendante dans une relation entre deux variables).
Axe vertical
L'axe vertical d'un plan cartésien se nomme l'axe des ordonnées , ou l'axe des y. Cet axe gradué est orienté du bas vers le haut du plan cartésien (on y indique la valeur de la variable dépendante dans une relation entre deux variables).
L'origine du repère
L'intersection des deux droites graduées est appelée origine du repère. Elle est notée O et ses coordonnées sont (0 ; 0).
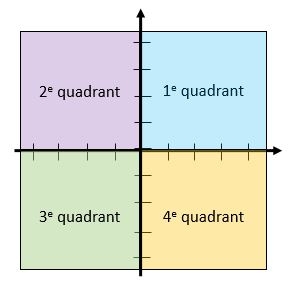
Les quatre quadrants
Les quatre régions du plan délimitées par ces deux axes sont appelées quadrants.
Ils sont numérotés dans le sens anti-horloger.
Coordonnées d'un point
La graduation des axes du plan cartésien permet de situer des points dans un plan. La position d'un point est donnée par un couple de nombres :
- le premier nombre s'appelle l'abscisse du point;
- le second nombre est appelé ordonnée du point.
Ensemble, ils forment un couple de nombres appelé les coordonnées du point et noté (x ; y).
Le premier nombre du couple correspond à la position horizontale du point (sa valeur sur l'axe des x ) alors que le deuxième nombre correspond à sa position verticale (sa valeur sur l'axe des y ).
Exemple : quelles sont les coordonnées du point A dessiné ci-dessous ?
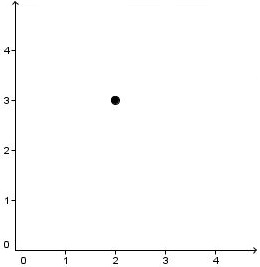
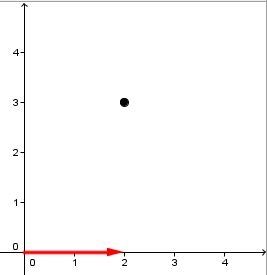
En partant de l'origine du repère, sur l'axe des x, il faut se déplacer de 2 unités vers la droite : l'abscisse du point A vaut "2".
De là, il faut monter de 3 unités vers le haut, parallèlement à l'axe des y, pour atteindre le point A : l'ordonnée du point A vaut "3".
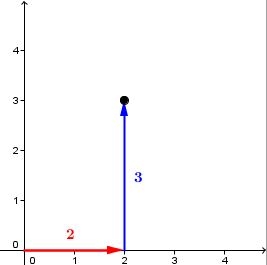
Conclusion : les coordonnées du point A sont (2 ; 3).
Notion de fonction
Notions de fonctions - Vocabulaire
Graphique d'une fonction affine
Image par une fonction
Réduction d’expressions comprenant des puissances
Réduction d’une puissance d’un produit
Soit le produit des nombres x et y, élevé à la troisième puissance.
En L.M. :
| (x . y)3 | |
| La définition de la puissance nous permet d’écrire : | = (x . y) . (x . y) . (x . y) |
| Vu l’associativité de la multiplication, on a : | = x . y . x . y . x . y |
| Vu la commutativité de la multiplication, on a : | = x . x . x . y . y . y |
| Vu l’associativité de la multiplication, on a : | = (x . x . x) . (y . y . y) |
| La définition de la puissance nous permet d’écrire : | = x3 . y3 |
| D’où : (x . y)3 = x3 . y3 | |
Nous retiendrons la formule :
| ∀ x, y ∈ Q ; ∀ n ∈ N : (x . y)n = xn . yn |
Réduction d’une puissance de puissance
Soit la 2e puissance de x élevée à la 3e puissance.
En L.M. : (x2)3
| La définition de la puissance nous permet d’écrire : | = (x2) . (x2) . (x2) |
| La définition de la puissance nous permet d’écrire : | = (x . x) . (x . x) . (x . x) |
| Vu l’associativité de la multiplication, on a : | = x . x . x . x . x . x |
| La définition de la puissance nous permet d’écrire : | = x6 |
D’où : (x2)3 = x6
Nous retiendrons la formule :
| ∀ x ∈ Q ; ∀ m, n ∈ N : (xm)n = xm . n |
Réduction d’un produit de puissances de même base
Soit le produit de la 2e puissance de x, par la 3e puissance de x
En L.M. : x2 . x3
| La définition de la puissance nous permet d’écrire : | = (x . x) . (x . x . x) |
| Vu l’associativité de la multiplication, on a : | = x . x . x . x . x |
| La définition de la puissance nous permet d’écrire : | = x5 |
D’où : x2 . x3 = x5
Nous retiendrons la formule :
| ∀ x ∈ Q ; ∀ m, n ∈ N : xm . xn = xm+n |
Réduction d’une puissance d’un quotient
Soit le quotient de x par y noté (x/y) élevée à la 3e puissance.
En L.M. : (x/y)3
| La définition de la puissance nous permet d’écrire : | = (x/y).(x/y).(x/y) |
| La règle du produit de fractions nous permet d’écrire : | = (x.x.x)/(y.y.y) |
| La définition de la puissance nous permet d’écrire : | = x3/y3 |
D’où : (x/y)3 = x3/y3
Nous retiendrons la formule :
| ∀ x ∈ Z ; ∀ y ∈ Z0 et ∀ n ∈ N : (x/y)n = xn/yn |
Réduction d’un quotient de puissances de même base
1er cas :
Soit le quotient de la 5e puissance de x, par la 3e puissance de x
En L.M. : x5/x3
| La définition de la puissance nous permet d’écrire : | = (x.x.x.x.x)/(x.x.x) |
| En appliquant la simplification de fractions, on a : | = (x.x)/1 |
| La définition de la puissance nous permet d’écrire : | = x2 |
D’où : x5/x3 = x2
2ème cas :
Soit le quotient de la 3e puissance de x, par la 5e puissance de x
En L.M. : x3/x5
| La définition de la puissance nous permet d’écrire : | = (x.x.x)/(x.x.x.x.x) |
| En appliquant la simplification de fractions, on a : | = 1/(x.x) |
| La définition de la puissance nous permet d’écrire : | = 1/x2 |
D’où : x3/x5 = 1/x2
Nous retiendrons la formule :
∀ x ∈ Z0 ; ∀ m, n ∈ N :
|
Remarque :
| x0 = 1 sauf si x = o (expression indéterminée) |
Les projections parallèles
Les ombres
Comme les rayons du soleil viennent d’un astre très éloigné, on peut les considérer comme parallèles. C’est pourquoi, quand un objet est exposé au soleil, tous les segments joignant chacun des points de l’objet au point de son ombre sont parallèles.
Propriétés des ombres au soleil
- Si un bâton est placé dans la direction des rayons du soleil, son ombre est réduite à sa base.
- Les ombres de deux bâtons parallèles entre-eux sont parallèles entre-elles. En plus :
- Si les bâtons ont même longueur, leurs ombres ont la même longueur ;
- Si un bâton a une longueur double de l’autre, l’ombre du 1er à une longueur double de celle du 2ème.
Règle graduée et projection parallèle
Les propriétés des projections parallèles (des ombres) expliquées ci-dessus peuvent s’appliquer à la droite graduée.
| Les projections parallèles conservent les abscisses |
- Remarque importante : si les abscisses sont conservées, les longueurs des segments ont été multipliées par un même nombre qui est le rapport entre la longueur d’un segment-image et la longueur de son correspondant.
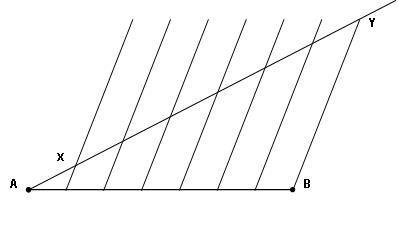
Division d’un segment en parties égales
On peut utiliser la propriété précédente pour diviser un segment en parties égales. Divise, par exemple, le segment [AB] en 7 parties égales :
- Trace une demi-droite d’origine A.
- Place sur cette demi-droite un point X.
- Reporte ce segment [AX] six fois au-delà de B.
- Appelle Y ce dernier point. Tu obtiens ainsi une graduation de [AY].
- Projette cette graduation sur [AB] parallèlement à la droite YB.
Compte tenu de la propriété énoncée ci-dessus, cette nouvelle graduation divise le segment [AB] en 7 parties égales.
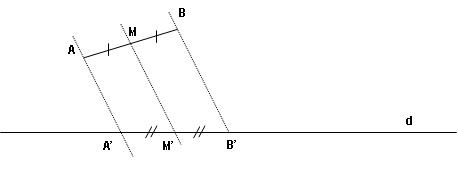
Conservation du milieu
Considérons le segment [AB] et le point M, milieu de ce segment. Si on projette ce segment sur une droite d dans une direction quelconque, on obtient le segment [A’B’] où M’ (image de M) est aussi le milieu de [A’B’] :
| Toute projection parallèle conserve le milieu |
Cette propriété appliquée au cas particulier des triangles porte le nom de théorème du milieu :
| Dans un triangle, la droite passant par le milieu d’un côté et parallèle à un autre côté passe par le milieu du troisième côté |
Simplification de fractions rationnelles
Simplifier une fraction rationnelle, c’est diviser les polynômes du numérateur et du dénominateur par tous leurs facteurs communs supposés non nuls.
En pratique, pour simplifier une fraction rationnelle, tu dois :
- factoriser numérateur et dénominateur ;
- énoncer les conditions d’existence ;
- diviser numérateur et dénominateur par leurs facteurs communs.
Exemple simple :
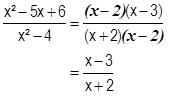Conditions d’existence : (x + 2)(x – 2) ≠ 0 <=> x ≠ -2 et x ≠ 2
Vidéo présentant quelques exemples (attention, les méthodes de factorisation évoquées sont différentes de celles vues en classe)