



A propos de quelques angles particuliers…
1. Angles adjacents
|
Deux angles sont adjacents ssi ils ont un côté commun et sont situés de part et d’autre de ce côté commun. |
2. Angles complémentaires
|
Deux angles sont complémentaires ssi la somme de leurs amplitudes est 90°. |
3. Angles supplémentaires
|
Deux angles sont supplémentaires ssi la somme de leurs amplitudes est 180°. |
4. Angles opposés par le sommet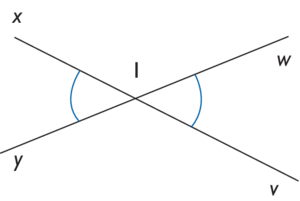
|
Deux angles sont opposés par le sommet ssi ils sont images l’un de l’autre par une symétrie centrale dont ce sommet est le centre. Ils ont la même amplitude |
5. Angles à côtés parallèles
|
Deux angles à côtés directement[1] parallèles ont la même amplitude. |
|
Deux angles à côtés inversement[2] parallèles ont la même amplitude. |
|
Deux angles ayant respectivement un côté directement parallèle et un côté inversement parallèle sont supplémentaires. |
6. Angles formés par deux parallèles et une sécante
Deux angles alternes-internes formés par deux droites parallèles et une sécante commune ont la même amplitude. |
|
|
|
|
7. Angles dans un triangle
|
|
|
|
Le calcul algebrique : Introduction
|
«Algèbre» est un mot d’origine arabe, directement tiré d’un ouvrage du savant perse Al-Khwarizmi (783 – 850 environ): Al Jabr. L’algèbre est alors la science des équations. Deux mille ans avant Jésus-Christ, les Babyloniens et les Egyptiens savent déjà résoudre des problèmes en utilisant les équations. Mais ils ne recourent pas encore à l’écriture littérale pour décrire leurs résolutions; ils les transcrivent à l’aide de phrases. C’est Diophante d’Alexandrie qui, au IIIè siècle av. J.-C., commence à introduire des symboles en utilisant des «abréviations» pour l’inconnue et pour les opérations. Aux VIIIè et IXè siècles, le monde arabo-musulman opère une synthèse de toutes les connaissances de l’époque et Al-Khwarizmi publie, en 825, son recueil Al Jabr, considéré comme la naissance officielle de l’algèbre. En Occident, les premières traductions de ce fameux traité apparaissent au XVè siècle, en Italie. Jusqu’alors, le manuel de référence est le livre Liber Abaci de l’Italien Léonard de Pise, dit Fibonacci (1170-1250). C’est le français François Viéte (1540-1603) qui donne à l’algèbre un nouvel essor en introduisant le symbolisme littéral. A la suite, Descartes (1596-1650) met définitivement en place les notations que nous employons aujourd’hui. |
1. Somme de termes identiques
Nous savons que :
5 + 5 + 5 + 5 = 4 . 5
Une somme de termes identiques peut s’écrire sous la forme d’un produit. Il en va de même pour le calcul algébrique :
a + a + a = 3a
ax + ax + ax + ax + ax = 5ax
b² + b² + b² = 3b²
Dans l’expression 3a ; "3" est appelé coefficient et indique le nombre de termes identiques.
2. Réduction de termes semblables
Exemples :
|
a + 3a + a + 2a = a + (a + a + a) + a + (a + a) = a + a + a + a + a + a + a = 7a |
4x² + x² = (x² + x² + x² + x²) + x² = x² + x² + x² + x² + x² = 5x² |
|
2ab + 3ab = (ab + ab) + (ab + ab + ab) = ab + ab + ab + ab + ab = 5ab |
2a + 5b + 9a + 6ab = 11a + 5b + 6ab |
Dans une somme algébrique, on n’additionne que les termes semblables, c’est-à-dire les termes qui ont la même partie littérale.
3. Produit de facteurs identiques
Nous savons que :
5 . 5 . 5 . 5 = 54
Un produit de facteurs identiques peut s’écrire sous la forme d’une puissance. Il en va de même pour le calcul algébrique :
a . a . a = a3
ax . ax . ax . ax . ax = (ax)5
b² . b² . b² = (b²)3
Dans l’expression a3 ; "3" est appelé exposant et indique le nombre de facteurs identiques.
4. Réduction de produits
Dans le calcul algébrique, pour réduire un produit, on utilise les propriétés de commutativité et d’associativité :
|
2a . 3b = 2.a . 3.b = (2.3) . (a.b) = 6ab |
5a . a = 5.a . a = 5 . (a.a) = 5a² |
2xy . x = 2.x.y . x = 2 . (x.x).y =2x²y |
5. La distributivité de la multiplication par rapport à l’addition et la soustraction
Dans nos recherches de formules du chapitre 1 (cours de 1ère), nous avons transformé certaines expressions pour prouver qu’elles étaient égales :
Exemple des nombres triangulaires (en négligeant la division par 2) :
n.(n + 1) = n² + n
|
|
n |
+ 1 |
|
n |
n² |
+ n |
En général, nous noterons :
| L.L. | La multiplication est distributive par rapport à l’addition. |
| L.M. | ∀ a, b et c ∈ Q : a.(b + c) = a.b + a.c |
Exemple de l’exercice 2b) (cours de 1ère) :
3 + 2.(n - 1) = 3 + 2n - 2
= 2n + 1
En général, nous noterons.
| L.L. | La multiplication est distributive par rapport à la soustraction. |
| L.M. | ∀ a, b et c ∈ Q : a.(b - c) = a.b - a.c |
 Carré de binômes
Carré de binômes
 Produit de binômes conjugués
Produit de binômes conjugués
Carré d'une somme de 2 termes
Quand tu effectues le carré d'une somme de 2 termes (un binôme), tu obtiens toujours 3 termes :
- le carré du premier terme : a²
- le double produit des deux termes : 2.a.b
- le carré du deuxième terme : b²
Donc :
| (a + b)² = a² + 2.a.b + b² |

Carré d'une différence de 2 termes
Quand tu effectues le carré d'une différence de 2 termes (un binôme), seul le double produit change de signe. En effet :
(a - b)² = [a + (-b)]²
- le premier terme reste : a²
- le double produit devient : 2.a.(-b) = -2.a.b
- le troisième terme reste : (-b)² = b²
Donc :
| (a - b)² = a² - 2.a.b + b² |
Remarque
Soit à calculer (-a - b)² :
(-a - b)² = (-a)² + 2.(-a).(-b) + (-b)² = a² + 2.a.b + b²
Tu obtiens le même trinôme que pour (a + b)², le double produit étant affecté du signe "+"!
Pour plus d'explications...
Exercices
 Exercices de rapidité : (a + b)²
Exercices de rapidité : (a + b)²
 Exercices de rapidité : (a - b)²
Exercices de rapidité : (a - b)²
Binômes conjugués
Deux binômes sont "conjugués" si un des deux termes de chaque expression est commun et si l'autre ne diffère que par son signe.
Par conséquent, le binôme (a + b) à pour conjugués :
- soit (a - b) ou (-b + a)
- soit (-a + b) ou (b - a)
Produit de deux binômes conjugués
En assemblant de deux façons différentes les deux trapèzes rectangles isométriques suivants :
.png)
|
Tu peux obtenir soit un rectangle :
|
= |
ou alors un carré auquel on a "enlevé un coin" :
|
Conclusion :
| (a + b).(a - b) = a² - b² |
Pour plus de détails...
Exercices
 Exercices de rapidité
Exercices de rapidité






 Dans tout triangle, la somme des amplitudes des angles intérieurs vaut 180°.
Dans tout triangle, la somme des amplitudes des angles intérieurs vaut 180°.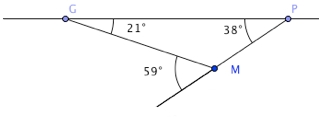 Dans tout triangle, l’amplitude d’un angle extérieur est égale à la somme des amplitudes des angles intérieurs non adjacents.
Dans tout triangle, l’amplitude d’un angle extérieur est égale à la somme des amplitudes des angles intérieurs non adjacents..png)
.png)