Comme quelque chose de barbant, qui peut devenir amusant ! Comme quelque chose de barbant, qui peut devenir amusant !
Symétrie centrale
-
Activité réalisée en classe
Après avoir plié 2x une feuille de papier (plis perpendiculaires) sur laquelle tu as dessiné une figure simple sur une des faces; découpé cette figure à travers toutes les épaisseurs et reproduit les motifs obtenus sur une feuille blanche, tu as obtenu :
Ilustration Géogébra
Définition
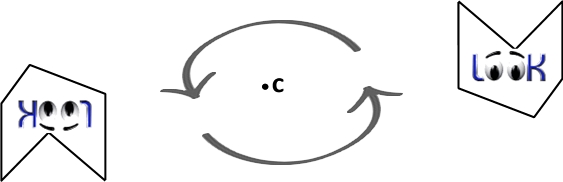
Pour passer du motif de droite au motif de gauche, tu peux simplement le faire tourner de 180° sans sortir du plan de la feuille...
C'est la raison pour laquelle nous dirons qu'une symétrie centrale est un déplacement.
|
Une symétrie centrale est un déplacement défini par un point appelé centre de symétrie. Ce point est le mileu du segment [objet-image]. |
Notation
ST (X) = Y signifie que le point Y est l’image du point X par la symétrie centrale S dont le centre est T
InvariantsL'observation des images construites, nous montre que la forme et la taille des figures n'ont pas changé durant leur déplacement.
Nous dirons que l'objet et son image sont isométriques.
En effet, les symétries centrales conservent :
- l'alignement des points
- la direction
- les distances
- l'aire des figures
- l'amplitude des angles
- la perpendicularité
- le parralélisme
Le sens des figures a, par contre, été inversé.
Construction de l'image d'un point (un triangle) par une symétrie centrale
Translation
-
Activité réalisée en classe
Après avoir plié 2x une feuille de papier (plis parallèles) sur laquelle tu as dessiné une figure simple sur une des faces; découpé cette figure à travers toutes les épaisseurs et reproduit les motifs obtenus sur une feuille blanche, tu as obtenu :
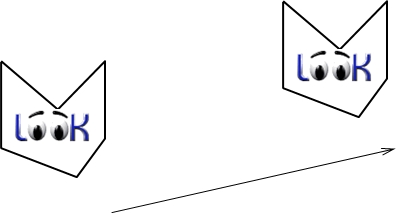
Ilustration Géogébra
Définition
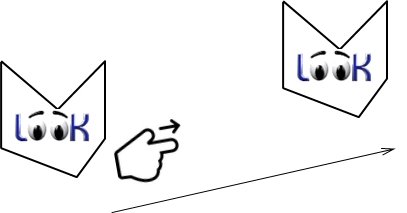
Pour passer du motif de gauche au motif de droite, tu peux simplement le faire glisser sans sortir du plan de la feuille...
C'est la raison pour laquelle nous dirons qu'une translation est un déplacement.
|
Une translation est un déplacement qui fait glisser les points du plan dans une même direction, dans un même sens et d'une même longueur (elle est définie par un vecteur). |
Notation
T
(X) = Y signifie que le point Y est l’image du point X par la translation de vecteur
L'observation des images construites, nous montre que la forme et la taille des figures n'ont pas changé durant leur déplacement.
Nous dirons que l'objet et son image sont isométriques.
En effet, les translations conservent :
- l'alignement des points
- la direction
- le sens
- les distances
- l'aire des figures
- l'amplitude des angles
- la perpendicularité
- le parralélisme
Construction de l'image d'un point (un triangle) par une symétrie centrale
Symétrie axiale
-
Activité réalisée en classe
Après avoir plié une feuille de papier sur laquelle tu as dessiné une figure simple sur une des faces; découpé cette figure à travers toutes les épaisseurs et reproduit les motifs obtenus sur une feuille blanche, tu as obtenu :
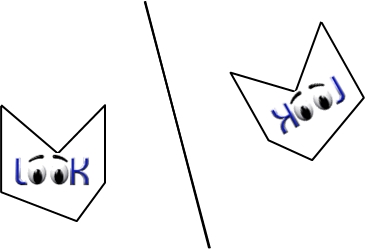
Définition
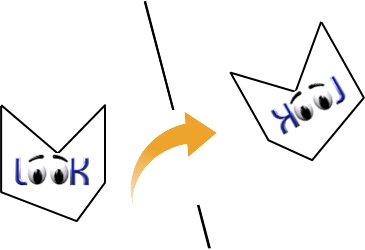
Pour passer du motif de gauche au motif de droite, tu ne peux pas simplement le faire glisser et tourner. Tu dois à tout pris le "sortir" du plan et le retourner...
C'est la raison pour laquelle nous dirons qu'une symétrie axiale est un retournement.
|
Une symétrie axiale est un retournement défini par un axe qui est perpendiculaire au segment [objet-image] en son milieu. |
Notation
Sa (X) = Y signifie que le point Y est l’image du point X par la symétrie axiale S dont l’axe est a
InvariantsL'observation des images construites, nous montre que la forme et la taille des figures n'ont pas changé durant leur déplacement.
Nous dirons que l'objet et son image sont isométriques.
En effet, les symétries axiales conservent :
- l'alignement des points
- les distances
- l'aire des figures
- l'amplitude des angles
- la perpendicularité
- le parralélisme
Construction de l'image d'un point (un triangle) par une symétrie axiale