Comme quelque chose de barbant, qui peut devenir amusant ! Comme quelque chose de barbant, qui peut devenir amusant !
Mettre la calculette en mode "degré"
Avant d'effectuer une opération avec ta calculette, tu dois d'abord vérifier si elle est bien en mode "degré" (petit "D" dans le haut de l'écran - voir vidéo ci-dessous).
passage en mode "degré"
Calculer les nombres trigonométriques d'un angle donné
- calcul du sinus de 18° : sin (18°) ≈ 0,309
- calcul du cosinus de 18° : cos (18°) ≈ 0,951
- calcul de la tangente de 18°52'16" : tan (18°52'16") ≈ 0,342
Calculer l'amplitude d'un angle à partir d'un de ses nombres trigonométriques
- Recherche de "α" sachant que sin α = 5/6
α = arcsin (5/6) = 56°26'33,68"
- Recherche de "β" sachant que cos β = 5/6
β = arcos (5/6) = 33°33'26,32"
- Recherche de "γ" sachant que tan γ = 2,35
γ = arctan (2,35) = 66°56'55,32"
Rappel important :
Comme la longueur de l'hypoténuse d'un triangle rectangle est toujours plus grande que celle d'un des côtés de l'angle droit, les rapports suivants :
côté opposé/hypoténuse et côté adjacent/hypoténuse
sont inférieurs à 1.
Donc, dans un triangle rectangle, pour tout angle aigu "α" :
0 < sinα < 1 |
0 < cosα < 1 |
Raison pour laquelle la calculette affiche "Math Error" pour une recherche du type :
α = arcsin (1,2) ou β = arcos (7/5)
Exposants négatifs et propriétés des puissances à exposants entiers
Les deux cas abordés en classe sont envisagés dans cette vidéo :
- la première partie de la vidéo explique pourquoi : x0 = 1, en partant de la définition des puissances ;
- la deuxième partie propose une approche intuitive pour le calcul avec des exposants négatifs (à partir de 16:20).
Explication sur le site de Khan Academy
Explications sur le site de Khan Academy
Exercices sur le site de Khan Academy
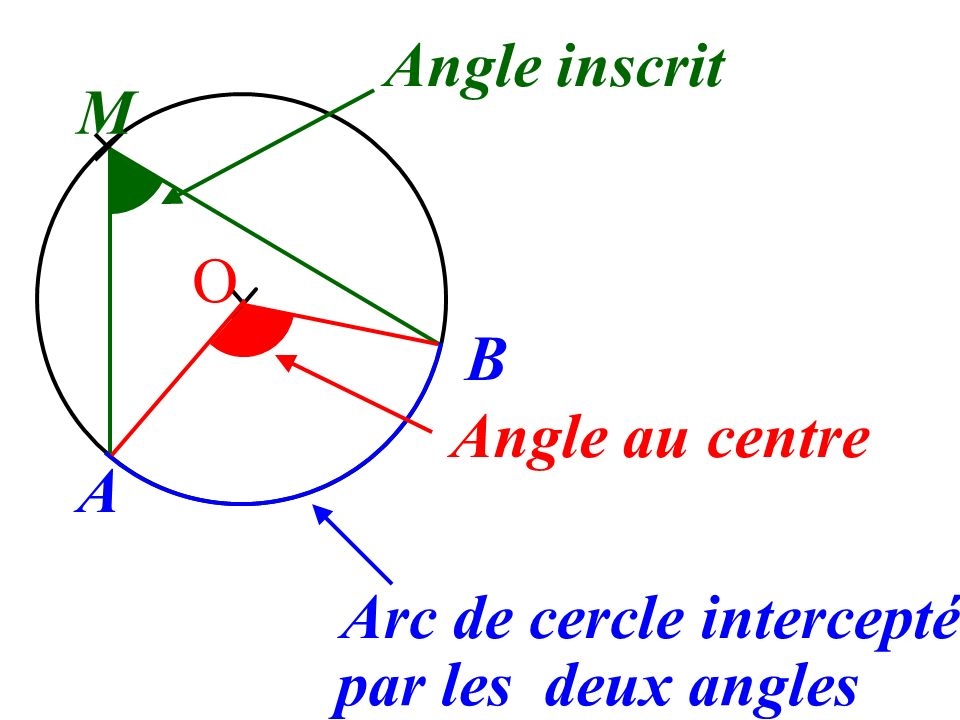
Définitions d'angles au centre et d'angles inscrits
Vidéo ci-dessous jusqu'à 2'34"
1. Angle au centre
| Un angle au centre d’un cercle est un angle dont le sommet est le centre du cercle. |
Exemple : AÔB est un angle au centre.
2. Angle inscrit
| Un angle inscrit à un cercle est un angle dont le sommet est un point du cercle et dont les côtés sont des cordes du cercle. |
Propriétés des angles inscrits, au centre,...
Tu retrouveras dans cette vidéo les propriétés suivantes :
1. Angles inscrits qui interceptent le même arc :
- lecture de 2'35" à 3'39" pour un angle au centre d'amplitude inférieure à 180°
- lecture de 6'19" à 9'05" pour un angle au centre d'amplitude supérieure à 180°
| Dans un cercle, des angles inscrits interceptant le même arc ont la même amplitude. |
2. Angle inscrit et angle au centre qui interceptent le même arc :
- lecture de 3'40" à 4'41"
| Dans un cercle, l’amplitude d’un angle au centre vaut le double de l’amplitude de l’angle inscrit interceptant le même arc. |
3. Triangles inscrits dans un demi-cercle
- lecture de 4'42" à 6'18"
| Tout triangle inscrit dans un demi-cercle est rectangle. |
Division par (x - a) et écriture : D : d.q + r
Les 7 premières minutes de la vidéo concernent la division par un binôme de la forme : (x - a). La suite est hors programme de 3ème année.